import networkx as nx 
import matplotlib.pyplot as plt 
import re
floppy = open("input25.txt", mode='r', encoding='utf-8')
thing =  floppy.readlines()
floppy.close()
sourcenode = []

for i, word in enumerate(thing):
    sourcenode.append(word[0:3])
    thing[i] = word[4:].split()

visual = []
for i, source in enumerate(sourcenode):
    for dest in thing[i]:
        visual.append([source,dest])
G = nx.Graph()
G.add_edges_from(visual)

nx.draw_networkx(G) 
plt.show()

import networkx as nx 
import matplotlib.pyplot as plt 

G = nx.Graph()
G.add_edges_from([['a','b'],['b','c'],['a','c'],['s','u']])
nx.draw_networkx(G) 
plt.show()

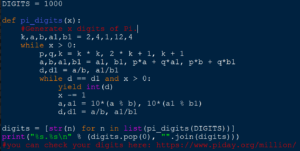
# Draw a Koch snowflake
from turtle import *

def koch(a, order):
    if order > 0:
        for t in [60, -120, 60, 0]:
            forward(a/3)
            left(t)
    else:
        forward(a)

# Test
koch(100, 0)
pensize(3)
koch(100, 1)

Now, we make a small change to the function koch:

    for t in [60, -120, 60, 0]:
            koch(a/3, order-1)
            left(t)

Completed code:

# Choose colours and size
color("sky blue", "white")
bgcolor("black")
size = 400
order = 0

# Ensure snowflake is centred
penup()
backward(size/1.732)
left(30)
pendown()

# Make it fast
tracer(100)
hideturtle()

begin_fill()

# Three Koch curves
for i in range(3):
    koch(size, order)
    right(120)

end_fill()

# Make the last parts appear
update()

Source.