int joyPin1 = A0; // slider variable connected to analog pin 0
int joyPin2 = A1; // slider variable connected to analog pin 1
int value1 = 0; // variable to read the value from the analog pin 0
int value2 = 0; // variable to read the value from the analog pin 1
void setup() {
pinMode(joyPin1, INPUT);
pinMode(joyPin2, INPUT);
Serial.begin(9600);
}
void loop() {
value1 = analogRead(joyPin1);
value2 = analogRead(joyPin2);
delay(100);
Serial.print("Pin1: ");
Serial.print(value1);
Serial.print(" Pin2: ");
Serial.println(value2);
}
Category Archives: source code
LED Images from the Shapeshifters
Arduino Serial Demo
void setup() {
Serial.begin(9600);
}
int i = 1;
void loop() {
Serial.println("Each line of code will be delayed by 1 second");
delay(1000);
Serial.println("Also, integer i will count upwards by one!");
delay(1000);
Serial.println(i);
i = i+1;
}
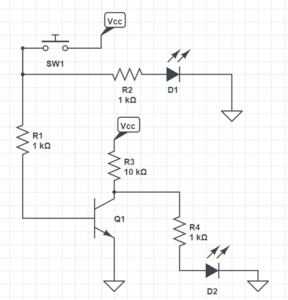
Building a NOT Gate
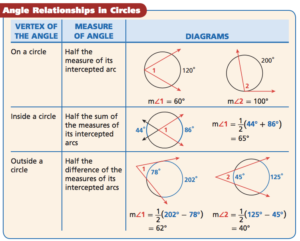
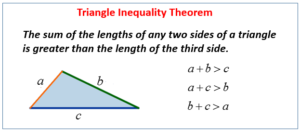
Geometry Formulas for EMCC
Rules of Inference
Area of an N-Sided Regular Polygon
Natas4
username: natas4
password: Z9tkRkWmpt9Qr7XrR5jWRkgOU901sw
Raspberry Pi Zero Header
RSA Encryption
woE7ewVfwoAzbwXCgC5iMyRvBTvCgGBiOy4=
public key: e=5, n=133
import random
import base64
'''
Euclid's algorithm to determine the greatest common divisor
'''
def gcd(a,b):
while b != 0:
c = a % b
a = b
b = c
return a
def egcd(a, b):
if a == 0:
return (b, 0, 1)
g, y, x = egcd(b%a,a)
return (g, x - (b//a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('No modular inverse')
return x%m
def encrypt(plaintext,keypair):
e,n = keypair
# Encrypt the plaintext
cipher = ''.join([chr(pow(ord(char),e,n)) for char in plaintext])
# Encode the ciphertext so it's more readable/sharable
encoded = base64.b64encode(cipher.encode('utf-8'))
return str(encoded,'utf-8')
def decrypt(ciphertext,keypair):
d,n = keypair
# Decode the text to the original format
decoded = base64.b64decode(ciphertext).decode('utf-8')
# Decrypt it
plain = (str(chr(pow(ord(char),d,n))) for char in decoded)
return ''.join(plain)
def generate_keypair(p,q,e=None):
n = p * q
#Phi is the totient of n
phi = (p-1)*(q-1)
#Choose an integer e such that e and phi(n) are coprime
if e is None:
e = random.randrange(1, phi)
#Use Euclid's Algorithm to verify that e and phi(n) are comprime
g = gcd(e, phi)
while g != 1:
e = random.randrange(1, phi)
g = gcd(e, phi)
#Now find the multiplicative inverse of e and phi to generate the private key
d = modinv(e, phi)
return ((e,n),(d,n))
#Only run this part if we're not running as an imported module
if __name__ == '__main__':
p = int(input("Enter prime number p: "))
q = int(input("Enter prime number q: "))
public, private = generate_keypair(p,q)
print("Your public key is the number pair of (e=" + str(public[0]) + ", n=" + str(public[1]) +").\n")
print("Your private key is the number pair of (d=" + str(private[0]) + ", n=" + str(private[1]) +").\n")
s = input("Enter your message: ")
encrypted = encrypt(s,public)
print("Encrypted message: " + encrypted)
decrypted = decrypt(encrypted,private)
print("Decrypt: " + decrypted)