The first thing we will be dong today is setting up individual GitHub Accounts. GitHub is the world’s biggest repository website. A repository is a place where coding projects are stored and updated, allowing many people to collaborate on a large coding project.
Please go to github.com and click “Sign Up” in the upper right corner.
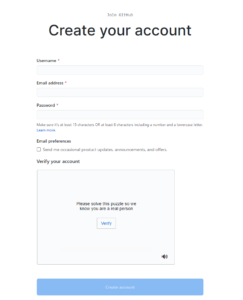
As your username please DO NOT use your real name.
Also, please keep in mind that your username will became the address of your website, so do not make it too long.
Next enter your IDEAL email address and a new password that is not the one you use for your IDEAL email. If you generally forget passwords, write this down on a piece of paper.
Next you will need to solve a small puzzle to “Verify your account” and prove that you are a person registering the account, not a bot.
On the next page, feel free to answer a reason that you are using Github. Your answers on this page can be whatever you choose.
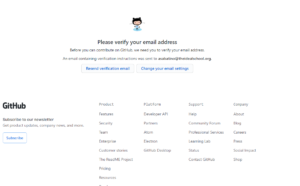
When you see this page:
You will need to go to your IDEAL email and look for an email from Github.
When you find it, please click “Verify email address”
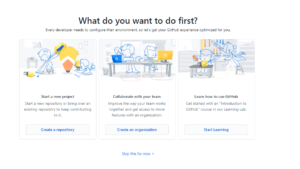
You will be taken to this page:
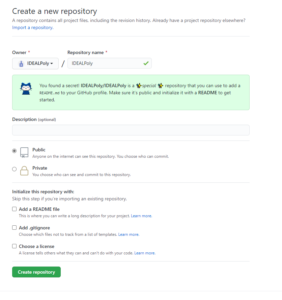
Please click “Create a repository”
The Repository name should MATCH YOUR GITHUB USERNAME EXACTLY, INCLUDING CAPITALIZATION WITH .GITHUB.IO. For example, if your username is Username123, your repository should be Username123.github.io This tells GitHub that you will be using this specific project for a website on GitHub Pages. It should say “You found a secret!” when you enter the right name for the repository. Also please make the repository Public.
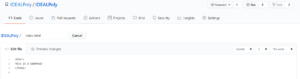
On the next page, please click “Create new file” to start your project:
Name your file “index.html” and try the code example below:
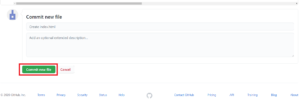
Scroll to the bottom and click “Commit new file” to save your changes:
Now you can visit your very own website at www.USERNAME.github.io.
You can see my example at www.idealpoly.github.io